Relational Algebra Introduction

Relational algebra didn’t get much attention outside of pure mathematics until Edgar F. Codd’s publication on the relational data in 1970. Codd proposed such algebra as a basis for database query languages. In expressive power, relational algebra is equivalent to relational calculus (and thus first-order logic). This result is known as Codd’s theorem named after E. F. Codd, the father of the relational model for database management. According to Wikipedia:

Codd’s theorem states that relational algebra and the domain-independent relational calculus queries, two well-known query languages for the relational model, are precisely equivalent in expressive power. That is, a database query can be formulated in one language if and only if it can be expressed in the other.

What is Algebra and Relational Algebra?

In mathematical terms, the “algebra” system consists of operands - variables or values from which new values can be constructed, and operators - symbols denoting procedures that construct new values from given values.

So, what is relational algebra? Relational algebra is:

• a formal description of how a relational database operates
• an interface to the data that is stored in a database
• The math under the roof of SQL operators

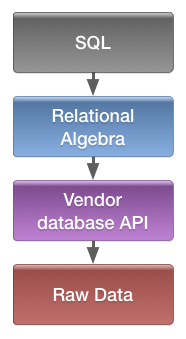
One more point here is that SQL operators are not always the same as operators in relational algebra. So, DBMS should take the SQL code, parse it, and then translate into relational algebra operations before applying to data. This process will be explained in more details later in the next post after we cover all the relational algebra operations.

Let’s define the core concepts:

• Relation - a set of tuples.
• Tuple - a collection of attributes describing entities
• Attribute - a data type
• Domain - a set of atomic data values
• Set - a mathematical definition for a collection of objects that contains no duplicates.

Relational algebra is a set of mathematical records and relations. Let’s say, a record is a set of attributes, where an attribute consists of name and value, and relation is a set of records.

Relational Algebra Operators are mathematical tools that can be used to retrieve queries by describing sequence operations on relations and schemas. Relational algebra is based on Sets Theory and is the key point in database logic.

Relational Algebra Operators are also mathematical functions that help retrieve queries by describing sequence operations on tables or even databases. A query is always composed of a number of relational algebra operators, with each of them composed of relations as variables and returning an individual abstraction as the end product.

A relation consists of a header and a number of tuples.

We talked about relations, but where is actually algebra? An algebra structure is just a set of operations that converts one member of the set into another member. For example, a unary operation turns one member into another, and a binary one combines two members to make a new one. If the members are relations, then we can call it relational algebra.

Relational algebra is equal to operations on relations. It can be called a math language for manipulations on sets of records. It’s a more abstract version of the SQL language, which in its turn is an abstraction to database vendor API.

Relational Algebra Core Operations

Algebra consists of operators and atomic operands. For instance, in the algebra of arithmetic, the atomic operands are variables and constants. The operators are common for arithmetic: addition, subtraction, multiplication, and division. Any algebra allows to build expressions by applying operators to atomic operands and/or other algebraic expressions.

Relational algebra is another type of algebra. Its atomic operands are the following:

1. Variables treated as relations
2. Constants - finite relations
3. A range of operators
   • Set operators – union, difference, and intersection
   • Operators that filter the relation – selection and projection
   • Operators for relation combination – Cartesian product and different types of joints
   • A special operation called renaming

Let me elaborate on the most frequently used and important operators below.

Projection Operation

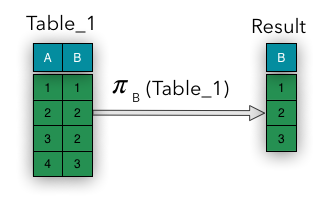
The Projection operation is a unary operation. It means that input and output of this operation is the only relation. This operation returns a set of tuples that contain a subset of attributes from the original relation. In other words, the Projection operation selects some columns and discards the others. The Projection operation is a kind of a vertical filter of the relation.

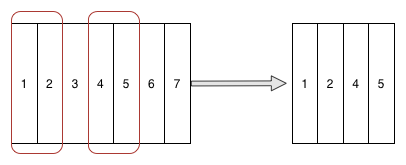
Please note, in the relational algebra of sets, duplicate tuples are always eliminated. The example of the projection operation is depicted below:

Selection (restriction)

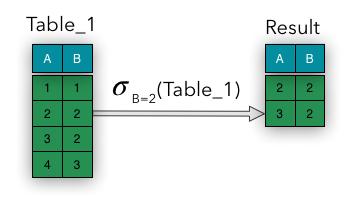
The Selection operation is also a unary operation. The Selection operation returns a subset of tuples from a relation that satisfies the required condition. In comparison to the Projection operation, it can be represented as a horizontal filter. It divides the input relation into two subsets: the tuples that satisfies the condition and those that don’t (this subset is discarded from the output relation).

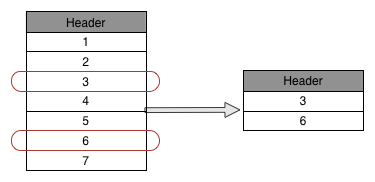
In the clause, the comparison operations could can be one of the following: $\lt \gt \le \ge \neq$. Clauses are connected by Boolean operators: and, or, not. The result size is $\mid \sigma_F(r) \mid \le \mid r \mid$

Steps for producingto produce the result of the Selection operator:

1. Condition $F$ is evaluated for each tuple
2. Any tuple for which $F(t)=true$ is added to the result set
3. Other tuples are discarded and not included in the result set

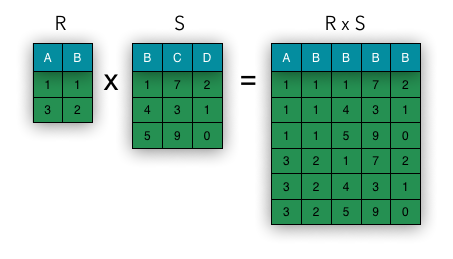
Cartesian Product

A Cartesian product (cross-product or product) is used to combine information from different relations. The notation is $R×S$. The final relation of a Cartesian product is the result of pairing a tuple from $R$ with each of the tuples from $S$ relation.

Join

In more cases than we want to take the product of two relations, we face the need to join them by pairing only those tuples that match in some way. The Join operation is used to combine related tuples from two relations into a single tuple. The Join is the most widely used operator in relational algebra that allows establishing connections between data from different relations.

There are two main versions of Join operations:

• Natural-join takes into account attribute names
• Theta-join is a specialized product containing only pairs that match in terms of a supplied condition called join-condition

Both Join operations are described with the $⨝$ symbol.

Natural Join

The simplest sort of match is the natural join of the $R$ and $S$ relations, where we pair only those tuples from $R$ and $S$ that agree on whatever attributes are common to the schemas of $R$ and $S$.

More precisely, let $A_1, A_2,…,A_n$ be all the attributes that are in both the schemas. of $R$ and the schema of $S$. Then a tuple $r$ from $R$ and a tuple $s$ from $S$ are successfully paired if and only if $r$ and $s$ agree on each of the attributes $A_1,A_2,…,A_n$. In other words, the tuples in the resulting relation are obtained by combining tuples in the operands with equal values on the common attributes.

More formally the semantics of the natural join can be defined as: $R \Join S = \lbrace r \cup s \mid r \in R \wedge s \in S \wedge F(r \cup s) \rbrace$

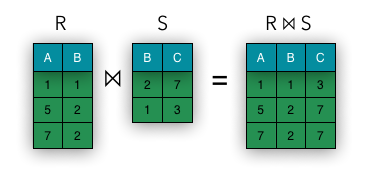
The resulted joins can be incomplete and even empty. If a tuple doesn’t have a counterpart in the other relation, then it isn’t included into the final join – such tuples are called “dangling” tuples. In some cases we might have no tuples that have counterpart, and the final result is called an empty join.

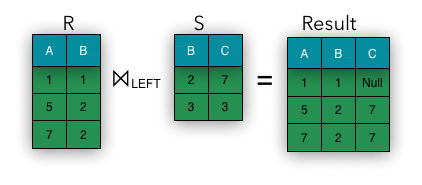
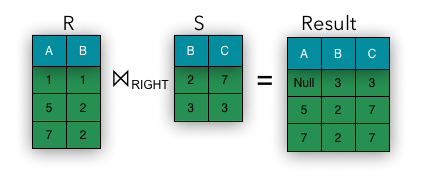
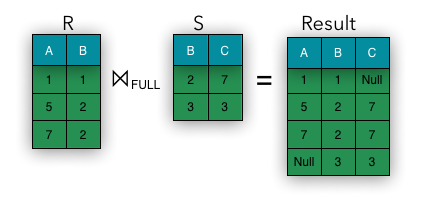
Outer Join

If we want to keep all information pieces from the operands, this requires a special type of join. Tuples that don’t have counterparts in other relation are pad with nulls. There are three types of outer joins:

• Full- tuples of all operands are padded
• Right – tuples on the right are padded
• Left – tuples on the left are padded

These operations are represented on the images below: